| n | F(n) | n | F(n) | n | F(n) |
| 0 | 0 | 1 | 1 | 2 | 1 |
| 3 | 2 | 4 | 3 | 5 | 5 |
| 6 | 8 | 7 | 13 | 8 | 21 |
| 9 | 34 | 10 | 55 | 11 | 89 |
| 12 | 144 | 13 | 233 | 14 | 377 |
| 15 | 610 | 16 | 987 | 17 | 1.597 |
| 18 | 2.584 | 19 | 4.181 | 20 | 6.765 |
| 21 | 10.946 | 22 | 17.711 | 23 | 28.657 |
| 24 | 46.368 | 25 | 75.025 | 26 | 121.393 |
| 27 | 196.418 | 28 | 317.811 | 29 | 514.229 |
| 30 | 832.040 | 31 | 1.346.269 | 32 | 2.178.309 |
| 33 | 3.524.578 | 34 | 5.702.887 | 35 | 9.227.465 |
| 36 | 14.930.352 | 37 | 24.157.817 | 38 | 39.088.169 |
| ... | ... | ... | ... | ... | ... |
Người ta chứng minh được rằng công thức tổng quát cho dãy Fibonacci là:
Fibonacci đã mô tả dãy các tổ tiên của một con ong đực như sau : (Loài ong có thể thụ tinh đơn tính hoặc lưỡng tính). Giả sử rằng:
- Nếu một trứng ong thụ tinh bởi chính con ong cái nó nở thành một con ong đực
- Tuy nhiên, nếu một trứng thụ tinh bởi một ong đực nó nở thành một con ong cái.
- Như vậy một con ong đực sẽ luôn có một mẹ, và một con ong cái sẽ có cả bố và mẹ.
Ta bắt đầu tính số các con ong tổ tiên của một con ong đực. Xét một con ong đực ở thế hệ thứ n.
- Trước một đời, thế hệ n-1: Con ong đực chỉ có một mẹ (1 ong cái).
- Trước hai đời, thế hệ n-2: Con ong cái đời n-1 có 2 bố mẹ, một ong bố (đực) và một ong mẹ (cái)(2 con ong: 1 đực+ 1 cái)) .
- Trước ba đời, thế hệ n-3: Con ong cái thế hệ n-2 lại có hai bố mẹ, một ong bố (đực) và một mẹ (cái), và con đực thế hệ n-2 có một mẹ (3 con ong: 1 ong đực + 2 ong cái)
- Trước bốn đời, thế hệ n-4: Hai con cái, mỗi con có 2 cha, mẹ và mỗi con đực có một mẹ (5 con ong: 2 ong đực 3 ong cái)
Tiếp tục quá trình này ta sẽ có một dãy số Fibonacci.
]Quan hệ với tỷ lệ vàng
Tỷ lệ vàng  (phi), được đinh nghĩa là tỷ số tỷ số khi chia đoạn thẳng thành hai phần sao cho tỷ lệ giữa cả đoạn ban đầu với đoan lớn hơn bằng tỷ số giữa đoạn lớn và đoạn nhỏ. Có thể chứng minh rằng nếu quy độ dài đoạn lớn về đơn vị thì tỷ lệ này là nghiệm dương của phương trình:
(phi), được đinh nghĩa là tỷ số tỷ số khi chia đoạn thẳng thành hai phần sao cho tỷ lệ giữa cả đoạn ban đầu với đoan lớn hơn bằng tỷ số giữa đoạn lớn và đoạn nhỏ. Có thể chứng minh rằng nếu quy độ dài đoạn lớn về đơn vị thì tỷ lệ này là nghiệm dương của phương trình:
 (phi), được đinh nghĩa là tỷ số tỷ số khi chia đoạn thẳng thành hai phần sao cho tỷ lệ giữa cả đoạn ban đầu với đoan lớn hơn bằng tỷ số giữa đoạn lớn và đoạn nhỏ. Có thể chứng minh rằng nếu quy độ dài đoạn lớn về đơn vị thì tỷ lệ này là nghiệm dương của phương trình:
(phi), được đinh nghĩa là tỷ số tỷ số khi chia đoạn thẳng thành hai phần sao cho tỷ lệ giữa cả đoạn ban đầu với đoan lớn hơn bằng tỷ số giữa đoạn lớn và đoạn nhỏ. Có thể chứng minh rằng nếu quy độ dài đoạn lớn về đơn vị thì tỷ lệ này là nghiệm dương của phương trình: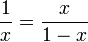 , hay tương đương
, hay tương đương 
chính là số  .
.
 .
.]Công thức dạng tường minh
Cũng như mọi dãy số xác định bởi công thức đệ quy tuyên tính, các số Fibonacci có thể tìm được công thức dạng tường minh.
Ta sẽ chứng minh (công thức Binet):
 , trong đó
, trong đó  là tỷ lệ vàng ở trên.
là tỷ lệ vàng ở trên.
Như vậy, từ hệ thức truy hồi Fibonacci ta có:
sẽ dẫn tới phương trình xác định tỷ lệ vàng
(là phương trình đa thức dặc trưng của hồi quy).
Chứng minh (bằng quy nạp):
Một nghiệm bất kỳ của phương trình trên thoả mãn tính chất  . Nhân hai vế với
. Nhân hai vế với  có:
có:
 . Nhân hai vế với
. Nhân hai vế với  có:
có:Chú ý rằng, theo định nghĩa  là một nghiệm của phương trình và nghiệm kia là
là một nghiệm của phương trình và nghiệm kia là  . Do đó:
. Do đó:
 là một nghiệm của phương trình và nghiệm kia là
là một nghiệm của phương trình và nghiệm kia là  . Do đó:
. Do đó:
 và
và
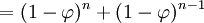
Bây giờ định nghĩa hàm:
 xác định với mọi số thực
xác định với mọi số thực 
Tất cả các hàm này tthỏa mãn hệ thức truy hồi Fibonacci, thật vậy:
Bây giờ chọn  và
và  . Tiếp tuc:
. Tiếp tuc:
 và
và  . Tiếp tuc:
. Tiếp tuc:và
những chứng minh ở trên chứng tỏ rằng
 với mọi n.
với mọi n.
Chú ý rằng, với hai giá trị khởi đầu bất kỳ của a,b, hàm  là công thức tường minh cho một loạt các hệ thức truy hồi.
là công thức tường minh cho một loạt các hệ thức truy hồi.
 là công thức tường minh cho một loạt các hệ thức truy hồi.
là công thức tường minh cho một loạt các hệ thức truy hồi.[sửa]Giới hạn của thương kế tiếp
Johannes Kepler, đã chứng minh sự hội tụ sau:
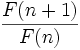 hội tụ tới tỷ lệ vàng
hội tụ tới tỷ lệ vàng  (phi)
(phi)
Thực ra kết quả này đúng với mọi cặp giá trị khởi đầu, trừ (0, 0).
Chứng minh:
Từ công thức tường minh, ta có, với mọi  :
:
 :
:

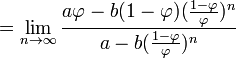
 ,
,
vì thế, như dễ dàng thấy, 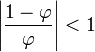 và như vậy
và như vậy 
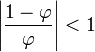 và như vậy
và như vậy 
Dạng ma trận
Việc giải một hệ thức truy hồi tổng quát dựa trên việc giải phương trình đặc trưng của nó. Lấy ví dụ như, cho hệ thức truy hồi dạng an = c1an-1+ c2an-2 + ... +ckan-k (1)
Khi đó nghiệm của hệ là r sẽ có dạng: rn = c1rn-1 + c2rn-2 +c3rn-3 +...+ckrn-k
Giải phương trình trên ta được các nghiệm phân biệt r1,r2,....,rn-1.Đồng thời ta có an=b1r1n +b2r2n +...+bn-1rn-1n (2)
Do vậy giải hệ phương trình (2) với a1,a2,.., an cho trước ta sẽ nhận được các giá trị b1,b2,... ,bn-1 , thay trở lại ta sẽ có phương trình tổng quát dành cho hệ thức truy hồi (1)
Trên đây chỉ là phương pháp giải Tổng Quát mà chưa nói rõ (chứng minh) về phương pháp giải, các bạn có thể tham khảo trong Giáo trình: Toán Rời Rạc của Lưu Đức Nghĩa - Nguyễn Tô Thành
[]Ứng dụng
[]Số Fibonacci trong tự nhiên
Dãy Fibonacci xuất hiện ở khắp nơi trong thiên nhiên. Những chiếc lá trên một nhành cây mọc cách nhau những khoảng tương ứng với dãy số Fibonacci. Các số Fibonacci xuất hiện trong những bông hoa. Hầu hết các bông hoa có số cánh hoa là một trong các số: 3,5,8,13,21,34,55 hoặc 89. Hoa loa kèn có 3 cánh, hoa mao lương vàng có 5 cánh, hoa phi yến thường có 8 cánh, hoa vạn cúc thọ có 13 cánh, hoa cúc tây có 21 cánh, hoa cúc thường có 34, hoặc 55 hoặc 89 cánh. Các số Fibonacci cũng xuất hiện trong các bông hoa hướng dương. Những nụ nhỏ sẽ kết thành hạt ở đầu bông hoa hướng dương được xếp thành hai tập các đường xoắn ốc: một tập cuộn theo chiều kim đồng hộ, còn tập kia cuộn ngược theo chiều kim đồng hồ. Số các đường xoắn ốc hướng thuận chiều kim đồng hồ thường là 34 còn ngược chiều kim đồng hồ là 55. Đôi khi các số này là 55 và 89, và thầm chí là 89 và 144. Tất ca các số này đều là các số Fibonacci kết tiếp nhau( tỷ số của chúng tiến tới tỷ số vàng).
]Các đẳng thức
- F(n + 1) = F(n) + F(n − 1)
- F(0) + F(1) + F(2) + ... + F(n) = F(n + 2) − 1
- F(1) + 2 F(2) + 3 F(3) + ... + n F(n) = n F(n + 2) − F(n + 3) + 2
[]Chuỗi lũy thừa
[]Tổng các nghịch đảo
Tổng vô hạn các nghịch đảo của các số Fibonacci có tính chất tương tự các hàm theta.
Giá trị mang tên hằng số nghịch đảo Fibonacci
đã được chứng minh là số vô tỷ bởi Richard André-Jeannin, nhưng chưa biết một biểu thức dạng chính xác của nó]
Tổng quát hóa
]Mở rộng cho các số âm
Dùng Fn-2 = Fn - Fn-1, có thể mở rộng các số Fibonacci cho các chỉ số nguyên âm. Khi đó ta có: ... -8, 5, -3, 2, -1, -1, 0, 1, 1, 2, 3, 5, 8, ... và F-n = -(-1)nFn.
[]Không gian vectơ
Thuật ngữ dãy Fibonacci cũng được dùng cho các hàm g từ tập các số nguyên tới một trường F thoả mãn g(n+2) = g(n) + g(n+1). Các hàm này có thể biểu diễn dưới dạng
- g(n) = F(n)g(1) + F(n-1)g(0),
do vậy các dãy Fibonacci hình thành một không gian vectơ với hàm F(n) và F(n-1) là một cơ sở.
Tổng quát hơn, giá trị của g có thể lấy trong một nhóm abel (xem như một z-module). Khi đó dãy Fibonacci là một Z-module 2 chiều.
[]Các dãy số nguyên tương tự
[]Các số Lucas
Đặc biệt, dãy Fibonacci L với L(1) = 1 và L(2) = 3 được gọi là số Lucas, theo tên của Edouard Lucas. Dãy Lucas đã được Leonhard Eulerđề cập đến năm 1748, trong Nhập môn giải tích vô hạn (Introductio in Analysin Infinitorum). Về ý nghĩa, các sô Lucas L(n) là luỹ thừa bậc ncủa tỷ lệ vàng
Các số Lucas quan hệ với các số Fibonacci theo hệ thức
Một tổng quát hoá của dãy Fibonacci là các dãy Lucas. Nó có thể định nghĩa như sau:
- U(0) = 0
- U(1) = 1
- U(n + 2) = PU(n + 1) − QU(n)
trong đó dãy Fibonacci là trường hợp đặc biệt khi P = 1 và Q = −1. Một dạng khác của các dãy Lucas bắt đầu với V(0) = 2, V(1) = P. Các dãy này có ứng dụng trong lý thuyết số để kiểm tra tính nguyên tố.
Các dãy Padovan là tương tự với hệ thức truy hồi P(n) = P(n − 2) + P(n − 3).
[]Các số Tribonacci
Các số tribonacci tương tự các số Fibonacci, nhưng thay vì khởi động với hai phần tử, dãy này khởi động với ba phân tử và mỗi số tiếp theo bằng tổng của ba phần tử đứng trước. Sau đây là một số sô tribonacci Bản mẫu:OEIS2C:
- 0, 0, 1, 1, 2, 4, 7, 13, 24, 44, 81, 149, 274, 504, 927, 1705, 3136, 5768, 10609, 19513, 35890, 66012, …
Giá trị của hằng số tribonacci là tỷ số (the ratio toward which adjacent tribonacci numbers tend). Nó là nghiệm của đa thứcx3 − x2 − x − 1, xấp xỉ 1.83929, và cũng thoả mãn phương trình x + x−3 = 2. Nó có vai trò quan trọng khi nghiên cứu khối snub.
Các số tribonacci cũng được cho bởi
ở đây cặp dấu ngoặc vuông ngoài là ký hiệu của hàm phần nguyên và
(Simon Plouffe, 1993).[1]
[]Các tổng quát hóa khác
Các đa thức Fibonacci là một tổng quát hoá khác của dãy Fibonacci.
Một dãy Fibonacci ngãu nhiên có thể xác định bằng việc ném đồng xu cho mỗi n trong dãy và lấy F(n)=F(n−1)+F(n−2) nếu đồng xu sấp và lấy F(n)=F(n−1)−F(n−2) nếu đồng xu ngửa.
Có thể định nghiã dãy "ngẫu nhiên Fibonacci" là dãy các số fn xác định theo đệ quy
- f0 = 1, f1 = 1, and

Hầu chắc chắn rằng căn bậc n của trị tuyệt đối của số hạng thứ n hội tụ về một hằng số khi n tăng vô hạn.
[]Số nguyên tố Fibonacci
Một số các số Fibonacci cúng là các số nguyên tố như Bản mẫu:OEIS2C: 2, 3, 5, 13, 89, 233, 1597, 28657, 514229, …. Chưa biết chắc rằng có vô hạn số nguyên tố Fibonacci không.
[]Các xâu (ký tự) Fibonacci
Tương tự với các biểu thức số, một xâu Fibonacci được định nghĩa đệ quy như sau:
 ,
,
trong đó dấu "+" ký hiệu cho phép ghép hai xâu. Dãy các xâu Fibonacci khởi đầu là:
- b, a, ab, aba, abaab, abaababa, abaababaabaab, …
Độ dài của mỗi xâu Fibonacci chính là số Fibonacci, và có một xâu Fibonacci tương ứng với mỗi số Fibonacci.
Các xâu Fibonacci cung cấp dữ liệu vào cho các minh dụ cho một vài thuật toán máy tính.
Dãy số Fibonacci rất đặc biệt này được một người Ý tên là Leonardo Fibonacci công bố năm 1202 và được biến hóa hầu như vô tận. Chính điều đó, đã thu hút được rất nhiều sự quan tâm cũng như làm chúng ta say mê nghiên cứu, khám phá các tính chất của nó.
Vậy dãy số Fibonacci là dãy số như thế nào?
Ban đầu, ông Fibonacci xét bài toán sau:
Giả sử có một cặp thỏ mắn đẻ cứ cuối mỗi tháng lại sinh ra một cặp mới. Nếu mỗi cặp mới đó cũng lại đẻ sau một tháng và nếu không có con nào bị chết cả thì sau một năm có bao nhiêu cặp thỏ?
Và đó là tiền thân của dãy số được xác định bằng cách liệt kê các phần tử như sau:
1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 …
Trong đó: các phần tử nằm trong dãy số này luôn luôn bằng tổng của 2 số liền trước nó. Nếu lấy tổng hay hiệu của các số liên tiếp bạn sẽ được một dãy số tương tự.
Vậy dãy số Fibonacci này có gì đặc biệt? Này nhé:
1. Điều đặc biệt đầu tiên:
Gọi An là số hạng thứ n trong dãy số, ta có:
An x An+1 = An-1 x An+2 ± 1
An x An+1 = An-2 x An+3 ± 2
An x An+1 = An-3 x An+4 ± 6
An x An+1 = An-4 x An+5 ± 15
Chúng ta hãy thử lại đẳng thức đầu tiên bằng cách chọn một số An bất kỳ (An là số ở vị trí thứ n của chuỗi), chẳng hạn 34. Ở đây, An = 34 (n = 9), An+1 = 55 , An-1 = 21 , An+2 = 89 . Ta có: 34 x 55 = 21 x 89 + 1. Các đẳng thức này được áp dụng trong toàn dãy số.
Lấy một cặp số bất kỳ khác, chẳng hạn 3 x 5 = (2 x 8 ) – 1.
Nếu lấy thêm các ví dụ khác nữa, bạn sẽ nhận ra rằng nếu n là số chẵn ta cộng 1. Nếu n là số lẻ ta trừ đi 1.
Bây giờ, ta xem xét đẳng thức thứ hai:
An x An+1 = An-2 x An+3 ± 2
Chọn An = 8, do đó 8 x 13 = 3 x 34 + 2. Tiếp theo chọn An = 34, ta có 34 x 55 = 13 x 144 – 2. Cũng tương tự như trên ta trong trường hợp An= 8 thì n =6 (chẵn) nên cộng 2, còn An = 34 thì n = 9 (lẻ), do đó trừ đi 2.
Những đẳng thức còn lại có thể kiểm chứng dễ dàng theo cách tương tự. Chú ý rằng, trong những số trên, những con số mà chúng ta thêm hay bớt theo thứ tự là:
±1 ±2 ±6 ±15 ±40 ±104 …
Hiệu số giữa những số này sẽ là:
1 4 9 25 64 …
Hay:
12 22 32 52 82
Đây lại là một điều thú vị nữa, bởi từ kết quả trên ta thấy hiệu của những con số được thêm vào (hay bớt đi) ở các đẳng thức trên không gì khác hơn là bình phương của các số hạng của dãy Fibonacci.
2. Điều bất ngờ kế tiếp:
Chúng ta tiếp tục xét và thử lại các đẵng thức sau:
3. Sự ngạc nhiên đến từ cách nhìn khác:
Bây giờ, nếu bạn đem nhân đôi một số hạng bất kỳ rồi trừ đi số hạng kế tiếp nó thì kết quả sẽ bằng số hạng đứng trước nó 2 vị trí:
Này nhé: với A5 = 5: 2 x 5 – 8 = 2 = A3
4. Điều thú vị có tên bình phương:
Bây giờ từ dãy Fibonacci ta tạo một dãy mới bằng cách đem bình phương các số hạng có trong dãy đó.
Với dãy Fibonacci:
1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 …
Ta có dãy số mới là:
1 1 4 9 25 64 169 441 1156 3025 7921 20736 54289 … (*)
Bây giờ, cộng mỗi cặp số liên tiếp trong dãy số mới. Ta có:
2 5 13 34 89 233 610 1597 …
dãy số sau cùng này chính là các số có mặt trong dãy Fibonacci ở các vị trí lẻ.
Tiếp theo, cũng từ dãy số bình phương (*), ta lấy hiệu của hai số cách nhau 1 số ở giữa, ta tiếp tục có:
3 8 21 55 144 377 987 …
đây cũng chính là những số có mặt trong dãy Fibonacci ở vị trí chẵn.
5. Ma thuật đến từ trò chơi tính nhẩm:
Nếu bạn biết được điều thú vị sau đây của dãy Fibonacci thì bạn sẽ luôn luôn thắng trong mọi cuộc đố vui tính nhẩm liên quan đến dãy số này. Và, vì thế, trò chơi này thường được gọi tên là tính nhẩm Fibonacci.
Viết dãy Fibonacci (F) theo dạng cột, và gạch dưới 1 số bất kỳ trong cột này. Tổng của các số nằm ở phía trên đường kẻ luôn luôn bằng số hạng thứ 2 sau đường kẻ trừ đi 1.
Giả sử bạn gạch dưới số 21. thì tổng các số phía trên đường kẻ là : 1 + 1 + 2 + 3 + 5 + 8 + 13 + 21 = 54 . Còn số hạng đứng dưới đường kẻ 2 vị trí là 55.
Hay bạn gạch dưới số 233 thì chắc chắn tồng các chữ số từ số ở vị trí đầu tiên đến số 233 sẽ phải bằng 610 – 1 = 609.
Do vậy, trò chơi này chắc chắn sẽ làm ngơ ngẩn những ai không quen thuộc với dãy số Fibonacci. Các con số ở đây dường như được chọn ngẫu nhiên, nhưng bí mật của trò ảo thuật nằm ở chỗ đáp số luôn luôn bằng số thứ hai sau nó trừ đi 1.
6. Định lý Pitagore trong dãy Fibonacci (F):
Bây giờ, nếu ta ký hiệu 4 số liên tiếp trong dãy F là a, b, c, d và gọi n là vị trí của a trong dãy số thì ta luôn có công thức tuyệt đẹp liên quan đến định lý Pitagore nổi tiếng. Đó là:
Hay ta luôn có:
Đây là một phương trình rất đặc biệt, được khám phá bởi Tiến sĩ Jekuthiel Ginsburg.
Chúng ta thử kiểm chứng lại kết quả này nhé. Ví dụ ta chọn dãy 4 số liên tiếp là 5 8 13 21. Ở đây n = 5. Ta có: . Rõ ràng, số 233 chính là số ở vị trí 2.5 + 3 = 13 trong dãy (F).
Bạn có thể kiểm chứng lại kết quả này bằng 1 dãy 4 số liên tiếp bất kỳ trong dãy (F).
Vậy là luôn luôn có những tam giác vuông ới độ dài các cạnh được tạo nên từ các số có mặt trong dãy (F).
7. Lại một điều thú vị được khám phá bởi TS Jekuthiel Ginsburg:
TS Jekuthiel Ginsburg khi nghiên cứu về dãy (F) ông đã tìm ra một điều hết sức đặc biệt. Số 89 ở vị trí thứ 11 của dãy (F) là 1 con số vô cùng quan trọng. Bởi lẽ, Số nghịch đảo của nó bằng tổng tất cả các số trong dãy (F). Điều này không thể giải thích nổi và nó được viết ra như sau:
8. Lại một điều kỳ thú của dãy (F) được khám phá bởi TS Jekuthiel Ginsburg:
Ông cho biết:
Trong 3 số liên tiếp của dãy (F) thì tổng lập phương của 2 số lớn trừ đi lập phương của số nhỏ nhất luôn luôn là 1 số trong dãy (F).
Ta thử kiểm chứng với 3 số liên tiếp bất kỳ. Giả sử: 5 8 13
Ồ ! 2584 chính là số ở vị trí thứ 18 trong dãy Fibonacci. Ngạc nhiên chưa!!!
9. Dãy Fibonacci chứa đựng tỷ số vàng:
Bạn đã bao giờ nghe đến “tỷ số vàng” chưa? Đó là con số tỷ lệ . Tỷ lệ này có được từ một hình chữ nhật có tính chất đặc biệt với độ thẩm mỹ rất thú vị. “Hình chữ nhật với chiều rộng là 1, chiều dài là x. Khi lấy đi một hình vuông có cạnh bằng 1 thì hình chữ nhật còn lại sẽ có các tỷ lệ như nhau so với hình chữ nhật ban đầu”.
Vì hình chữ nhật mới có chiều rộng là x – 1 và chiều dài là 1 nên sự tương đương các tỷ lệ có nghĩa là:
Từ đó, ta có được “tỷ số vàng” . Hiện nay, Tỷ lệ nàyđược sử dụng rộng rãi trong lĩnh vực xây dựng và mỹ thuật.
Trở lại với dãy số Fibonacci. Thật kỳ lạ khi thấy rằng tỷ số này có mặt suốt trong dãy. Thật vậy, khi nhân lần lượt các số trong dãy với tỷ số vàng , bạn sẽ tiến càng lúc càng chính xác đến giá trị của số kế tiếp.
Này nhé:
1 x 1.618033989… = 1.618033989 = 2 – 0.381966011
2 x 1.618033989… = 3.236067977 = 3 + 0.236067977
3 x 1.618033989… = 4.854101966 = 5 – 0.145898033
5 x 1.618033989… = 8.090169944 = 8 + 0.090169944
8 x 1.618033989… = 12.94427191 = 13 – 0.05572809
13 x 1.618033989… = 21.03444185 = 21 + 0.03444185
21 x 1.618033989… = 33.97871376 = 34 – 0.021286236
34 x 1.618033989… = 55.01315562 = 55 + 0.01315562
55 x 1.618033989… = 88.99186938 = 89 – 0.008130619
89 x 1.618033989… = 144.005025 = 144 + 0.005025
144 x 1.618033989… = 232.9968944 = 233 – 0.003105622
233 x 1.618033989… = 377.0019194 = 377 + 0.0019194
377 x 1.618033989… = 609.9988138 = 610 – 0.001186246
610 x 1.618033989… = 987.0007331 = 987 + 0.0007331
987 x 1.618033989… = 1596.999547 = 1597 – 0.00045312
987 x 1.618033989… = 1596.999547 = 1597 – 0.00045312
1597 x 1.618033989… = 2584.00028 = 2584 + 0.00028
Dãy số Fibonacci rất đặc biệt này được một người Ý tên là Leonardo Fibonacci công bố năm 1202 và được biến hóa hầu như vô tận. Chính điều đó, đã thu hút được rất nhiều sự quan tâm cũng như làm chúng ta say mê nghiên cứu, khám phá các tính chất của nó.
Vậy dãy số Fibonacci là dãy số như thế nào?
Ban đầu, ông Fibonacci xét bài toán sau:
Giả sử có một cặp thỏ mắn đẻ cứ cuối mỗi tháng lại sinh ra một cặp mới. Nếu mỗi cặp mới đó cũng lại đẻ sau một tháng và nếu không có con nào bị chết cả thì sau một năm có bao nhiêu cặp thỏ?
Và đó là tiền thân của dãy số được xác định bằng cách liệt kê các phần tử như sau:
1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 …
Trong đó: các phần tử nằm trong dãy số này luôn luôn bằng tổng của 2 số liền trước nó. Nếu lấy tổng hay hiệu của các số liên tiếp bạn sẽ được một dãy số tương tự.
Vậy dãy số Fibonacci này có gì đặc biệt? Này nhé:
1. Điều đặc biệt đầu tiên:
Gọi An là số hạng thứ n trong dãy số, ta có:
An x An+1 = An-1 x An+2 ± 1
An x An+1 = An-2 x An+3 ± 2
An x An+1 = An-3 x An+4 ± 6
An x An+1 = An-4 x An+5 ± 15
Chúng ta hãy thử lại đẳng thức đầu tiên bằng cách chọn một số An bất kỳ (An là số ở vị trí thứ n của chuỗi), chẳng hạn 34. Ở đây, An = 34 (n = 9), An+1 = 55 , An-1 = 21 , An+2 = 89 . Ta có: 34 x 55 = 21 x 89 + 1. Các đẳng thức này được áp dụng trong toàn dãy số.
Lấy một cặp số bất kỳ khác, chẳng hạn 3 x 5 = (2 x 8 ) – 1.
Nếu lấy thêm các ví dụ khác nữa, bạn sẽ nhận ra rằng nếu n là số chẵn ta cộng 1. Nếu n là số lẻ ta trừ đi 1.
Bây giờ, ta xem xét đẳng thức thứ hai:
An x An+1 = An-2 x An+3 ± 2
Chọn An = 8, do đó 8 x 13 = 3 x 34 + 2. Tiếp theo chọn An = 34, ta có 34 x 55 = 13 x 144 – 2. Cũng tương tự như trên ta trong trường hợp An= 8 thì n =6 (chẵn) nên cộng 2, còn An = 34 thì n = 9 (lẻ), do đó trừ đi 2.
Những đẳng thức còn lại có thể kiểm chứng dễ dàng theo cách tương tự. Chú ý rằng, trong những số trên, những con số mà chúng ta thêm hay bớt theo thứ tự là:
±1 ±2 ±6 ±15 ±40 ±104 …
Hiệu số giữa những số này sẽ là:
1 4 9 25 64 …
Hay:
12 22 32 52 82
Đây lại là một điều thú vị nữa, bởi từ kết quả trên ta thấy hiệu của những con số được thêm vào (hay bớt đi) ở các đẳng thức trên không gì khác hơn là bình phương của các số hạng của dãy Fibonacci.
2. Điều bất ngờ kế tiếp:
Chúng ta tiếp tục xét và thử lại các đẵng thức sau:
3. Sự ngạc nhiên đến từ cách nhìn khác:
Bây giờ, nếu bạn đem nhân đôi một số hạng bất kỳ rồi trừ đi số hạng kế tiếp nó thì kết quả sẽ bằng số hạng đứng trước nó 2 vị trí:
Này nhé: với A5 = 5: 2 x 5 – 8 = 2 = A3
4. Điều thú vị có tên bình phương:
Bây giờ từ dãy Fibonacci ta tạo một dãy mới bằng cách đem bình phương các số hạng có trong dãy đó.
Với dãy Fibonacci:
1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 …
Ta có dãy số mới là:
1 1 4 9 25 64 169 441 1156 3025 7921 20736 54289 … (*)
Bây giờ, cộng mỗi cặp số liên tiếp trong dãy số mới. Ta có:
2 5 13 34 89 233 610 1597 …
dãy số sau cùng này chính là các số có mặt trong dãy Fibonacci ở các vị trí lẻ.
Tiếp theo, cũng từ dãy số bình phương (*), ta lấy hiệu của hai số cách nhau 1 số ở giữa, ta tiếp tục có:
3 8 21 55 144 377 987 …
đây cũng chính là những số có mặt trong dãy Fibonacci ở vị trí chẵn.
5. Ma thuật đến từ trò chơi tính nhẩm:
Nếu bạn biết được điều thú vị sau đây của dãy Fibonacci thì bạn sẽ luôn luôn thắng trong mọi cuộc đố vui tính nhẩm liên quan đến dãy số này. Và, vì thế, trò chơi này thường được gọi tên là tính nhẩm Fibonacci.
Viết dãy Fibonacci (F) theo dạng cột, và gạch dưới 1 số bất kỳ trong cột này. Tổng của các số nằm ở phía trên đường kẻ luôn luôn bằng số hạng thứ 2 sau đường kẻ trừ đi 1.
Giả sử bạn gạch dưới số 21. thì tổng các số phía trên đường kẻ là : 1 + 1 + 2 + 3 + 5 + 8 + 13 + 21 = 54 . Còn số hạng đứng dưới đường kẻ 2 vị trí là 55.
Hay bạn gạch dưới số 233 thì chắc chắn tồng các chữ số từ số ở vị trí đầu tiên đến số 233 sẽ phải bằng 610 – 1 = 609.
Do vậy, trò chơi này chắc chắn sẽ làm ngơ ngẩn những ai không quen thuộc với dãy số Fibonacci. Các con số ở đây dường như được chọn ngẫu nhiên, nhưng bí mật của trò ảo thuật nằm ở chỗ đáp số luôn luôn bằng số thứ hai sau nó trừ đi 1.
6. Định lý Pitagore trong dãy Fibonacci (F):
Bây giờ, nếu ta ký hiệu 4 số liên tiếp trong dãy F là a, b, c, d và gọi n là vị trí của a trong dãy số thì ta luôn có công thức tuyệt đẹp liên quan đến định lý Pitagore nổi tiếng. Đó là:
Hay ta luôn có:
Đây là một phương trình rất đặc biệt, được khám phá bởi Tiến sĩ Jekuthiel Ginsburg.
Chúng ta thử kiểm chứng lại kết quả này nhé. Ví dụ ta chọn dãy 4 số liên tiếp là 5 8 13 21. Ở đây n = 5. Ta có: . Rõ ràng, số 233 chính là số ở vị trí 2.5 + 3 = 13 trong dãy (F).
Bạn có thể kiểm chứng lại kết quả này bằng 1 dãy 4 số liên tiếp bất kỳ trong dãy (F).
Vậy là luôn luôn có những tam giác vuông ới độ dài các cạnh được tạo nên từ các số có mặt trong dãy (F).
7. Lại một điều thú vị được khám phá bởi TS Jekuthiel Ginsburg:
TS Jekuthiel Ginsburg khi nghiên cứu về dãy (F) ông đã tìm ra một điều hết sức đặc biệt. Số 89 ở vị trí thứ 11 của dãy (F) là 1 con số vô cùng quan trọng. Bởi lẽ, Số nghịch đảo của nó bằng tổng tất cả các số trong dãy (F). Điều này không thể giải thích nổi và nó được viết ra như sau:
8. Lại một điều kỳ thú của dãy (F) được khám phá bởi TS Jekuthiel Ginsburg:
Ông cho biết:
Trong 3 số liên tiếp của dãy (F) thì tổng lập phương của 2 số lớn trừ đi lập phương của số nhỏ nhất luôn luôn là 1 số trong dãy (F).
Ta thử kiểm chứng với 3 số liên tiếp bất kỳ. Giả sử: 5 8 13
Ồ ! 2584 chính là số ở vị trí thứ 18 trong dãy Fibonacci. Ngạc nhiên chưa!!!
9. Dãy Fibonacci chứa đựng tỷ số vàng:
Bạn đã bao giờ nghe đến “tỷ số vàng” chưa? Đó là con số tỷ lệ . Tỷ lệ này có được từ một hình chữ nhật có tính chất đặc biệt với độ thẩm mỹ rất thú vị. “Hình chữ nhật với chiều rộng là 1, chiều dài là x. Khi lấy đi một hình vuông có cạnh bằng 1 thì hình chữ nhật còn lại sẽ có các tỷ lệ như nhau so với hình chữ nhật ban đầu”.
Vì hình chữ nhật mới có chiều rộng là x – 1 và chiều dài là 1 nên sự tương đương các tỷ lệ có nghĩa là:
Từ đó, ta có được “tỷ số vàng” . Hiện nay, Tỷ lệ nàyđược sử dụng rộng rãi trong lĩnh vực xây dựng và mỹ thuật.
Trở lại với dãy số Fibonacci. Thật kỳ lạ khi thấy rằng tỷ số này có mặt suốt trong dãy. Thật vậy, khi nhân lần lượt các số trong dãy với tỷ số vàng , bạn sẽ tiến càng lúc càng chính xác đến giá trị của số kế tiếp.
Này nhé:
1 x 1.618033989… = 1.618033989 = 2 – 0.381966011
2 x 1.618033989… = 3.236067977 = 3 + 0.236067977
3 x 1.618033989… = 4.854101966 = 5 – 0.145898033
5 x 1.618033989… = 8.090169944 = 8 + 0.090169944
8 x 1.618033989… = 12.94427191 = 13 – 0.05572809
13 x 1.618033989… = 21.03444185 = 21 + 0.03444185
21 x 1.618033989… = 33.97871376 = 34 – 0.021286236
34 x 1.618033989… = 55.01315562 = 55 + 0.01315562
55 x 1.618033989… = 88.99186938 = 89 – 0.008130619
89 x 1.618033989… = 144.005025 = 144 + 0.005025
144 x 1.618033989… = 232.9968944 = 233 – 0.003105622
233 x 1.618033989… = 377.0019194 = 377 + 0.0019194
377 x 1.618033989… = 609.9988138 = 610 – 0.001186246
610 x 1.618033989… = 987.0007331 = 987 + 0.0007331
987 x 1.618033989… = 1596.999547 = 1597 – 0.00045312
987 x 1.618033989… = 1596.999547 = 1597 – 0.00045312
1597 x 1.618033989… = 2584.00028 = 2584 + 0.00028
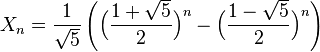






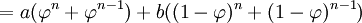
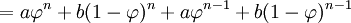






![T(n) = \left[ 3 \, b \frac{\left(\frac{1}{3} \left( a_{+} + a_{-} + 1\right)\right)^n}{b^2-2b+4} \right]](http://upload.wikimedia.org/math/9/9/1/9917cded587ee2970e64a25a64489627.png)


![\sqrt[n]{|f_n|} \to 1.13198824\dots \mbox{ as } n \to \infty.](http://upload.wikimedia.org/math/8/d/d/8dda0f7d3437cfea9cd8245fe370d43e.png)
No comments:
Post a Comment